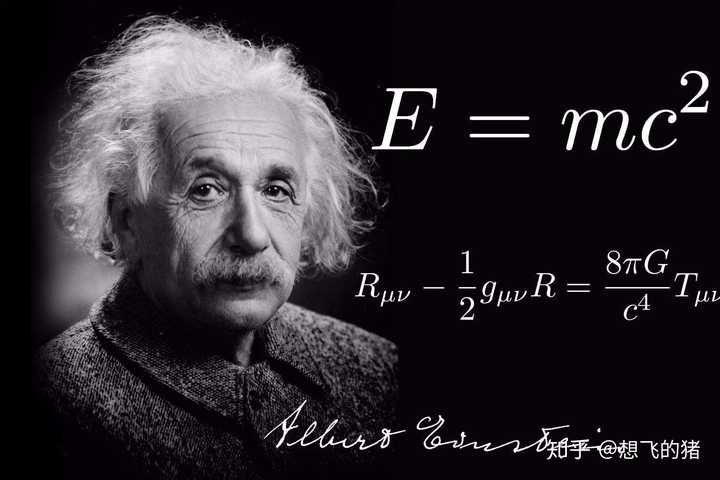狭义相对论公式:
1:设一个物体质量为M,它所在的参照系相对于另一个参照系的速度为v
则它的质量相对于另一个参照系变为M1,
M1和M之间的关系为M1=M/√[1-(v/c)^2]
2:类似的,设一个物体的长度为L,它相对于另一个参照系的长度为L1
则:L1=L×√[1-(v/c)^2]
c为光速,在任何一个参照系看来,c都是不变的,这是光速不变原理
3:生命周期变化公式:T1=T/√[1-(v/c)^2]
4:设光子能量为E,动量为p,动质量为m,则:E^2=p^2c^2+m^2c^4
像这样的公式还有很多.
广义相对论公式:
1:设一个物体在一个质量大的星球附近,这个星球质量为M
物体原本的质量为m,在这个星球(有可能为黑洞)所产生的强引力场中它的质量为m1,则m1=m/√[1-2GM/Rc^2]
2:类似的有:L1=L√[1-2GM/Rc^2]
3:生命周期变化公式:T1=T/√[1-2GM/Rc^2]
4:爱因斯坦引力场方程:Gμν=8πGTμν/c^4,(μν是下标)
5:宇宙临界密度公式:ρc=3H^2/8πG,(c为下标,H为哈勃常量)
关于量子力学的公式:
爱因斯坦光电方程:hν=W-Ek,W为溢出功,Ek为初动能)
光子能量方程:E=hν,(ν为光子频率)
关于布朗运动的公式
△^2x=(RT/NA)·(t/3πηγ),(△x表示微粒的运动位移,△^2表示△的平方,NA为阿伏加德罗常数)
爱因斯坦公式:△ E=(△m)c²,式中E为能量,m为质量,c为光速,是一个以时空为自变量、以度规为因变量的带有椭圆型约束的二阶双曲型偏微分方程。它是一切物质运动速度的最大极限,是1905年物理学家爱因斯坦创建的。
从公式中可以看出,物体的能量每增加△E,相应的惯性质量也必定增加△m;反之,每减少△m 的质量,就意味着释放出△E的巨大能量。也就是说:质量与能量是等价的,是可以相互转化的,少量的质量能够转换为十分巨大的能量。这是一个惊天动地的理论,它揭开了宇宙的一个巨大奥妙,为原子能的利用奠定了理论基础。因此,这一公式被后人称为“改变世界的方程”。